Module 4 – Part 7: Fingertip Fumbles…
Benji
Fingertip Fumbles…
All the other stuff aside, I think THIS is my favorite thing to do with the faro. It’s so devious but so fun.
Marlo put out a booklet titled ‘Faro Notes’, in which he discussed a routine called ‘Fingertip Miracle.’
Tucked away inside it is a routine called ‘Fingertip Miracle’, which became one of the inspirations for Juan Tamariz’ Mnemonicosis (along with Vernon’s ‘The Trick that Cannot Be Explained.)
The idea behind Fingertip Miracle is to start in Faro 5, let someone peek at a card after each shuffle, and then once we’re in Faro 8 (aka our memorized order) we can reveal the cards in any number of surprising ways—since we know their position within the memorized deck.
Anyway, when I read this I wondered what else we could do with this principle.
Let’s get reacquainted with our charts from Expert Card Technique…
These bad boys are the inspiration for a lot of the ideas in this section, so keep ‘em handy.
So, let’s discuss 3 ideas I’ve had based on Marlo’s Fingertip Miracle.
Marlo was a beast, so I’m not going to argue with his naming convention, but for our purposes, I’ll refer to my creations as the ‘Fingertip Fumbles.’
But don’t let that fool you…I’d like to think there’s some pretty sneaky stuff going on in them.
NOTE: In this section, I’ll just be referring to ‘faros’. By this I mean Out Faros that you can accomplish either via the standard handling or my ‘EZ’ method.
Fingertip Fumble #1
In this effect, three people pick a card (or one person picks 3 cards) in between shuffles. Even though there’s no way we could know the cards…we do. And then, we reveal that something magical has occurred with their cards.
Sorry I couldn’t be more specific with that description. The fact of the matter is simply that the final reveal on this changes each time.
Here’s the basic overview of the method:
We start in faro 5 and ‘count’ how many cards we spread before they pick one, which they replace where they took it from. We then know the identity of that card. We faro shuffle into faro 6 and do the same again. We then shuffle into faro 7 and do the same again. Finally we shuffle into faro 8—our memorized order. Once we’re in our memorized order, we can reveal their cards based on their location in the deck.
That’s the ‘bird’s eye view’ look at the method.
To really get granular, let’s break down what happened when I performed this effect on Jacob:
Referring to the first chart, we’re going to start this effect in faro 5, or the ‘5th shuffle.’
As I move the cards from my left hand to my right, I track our progress into the chart for the 5th shuffle. If you watch me do this, you’ll see I do this without reversing the order—so we maintain our stack.
In the Live Session, I took the easy route and just had the chart open for reference, however, it’s not a huge task to mentally track the route through the fifth faro (it starts at 1 and increases by 8 each card—1, 9, 17, 25, 33, 41, 49. Then jumps back to 6, 14, 22, 30, 38, 46.)
That’s 13 cards, which is usually enough time for them to call out stop.
Here’s an important point: I would usually handle this by asking them to ‘tell me stop’ rather than ‘pick a card.’
Asking them to ‘pick a card’ invites them into your space and gives them permission to pull a random card out of the deck. Asking them to tell you stop can both seem fairer (slow, there are no funny moves) but it also makes it highly likely they’ll stop you within the first 13 cards.
Furthermore, I don’t generally find it to be a suspicious thing to be passing the cards slowly since this is a ‘tell me when to stop’ procedure rather than a ‘pick a card’ procedure.
If you want to spread faster, you could use Elmsley’s ‘3-3-2-2’ idea. In this count, you push off 3 cards as one, then 3 again, then 2, and then 2 again. This allows you to count through 10 cards fast and without it being obvious that you’re counting. But again, I don’t have a problem with it since you said ‘tell me when to stop’ and it feels natural to be passing cards at a slower pace.
If they don’t stop you within the first 13 cards, we also know the next set of numbers in a pinch: they start at 3 and once again progress by 8. (3, 11, 19, 27, 35, 43, 51.)
Once we know their number, we can just convert that number into the card. Jacob stopped me on 30, which would have been the 5C.
Once they’ve looked at their card, we can have them return them to the same spot they removed it from.
Give the deck another faro shuffle, which moves us into Faro 6 (the ‘6th shuffle’ in the chart.)
We’ll do the same thing again now. The 6th shuffle starts at 1 and increases by 4 each time (1, 5, 9, 13, 17, 21, 25, 29, etc.). Once it maxes out, it starts again at 2 (2, 6, 10, 14, 18, etc.).
Once again, we’ll know their card once they call out ‘stop.’ Jacob stopped me at the 25th card, which would have been the 5D.
We’ll do this one last time in faro 7. This one is the easiest to track since it starts at 1 and runs through the odd numbers (1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, etc.)
In this case, Jacob stopped me at 19, which would have been the 2D.
Now we give the deck one more faro, which brings us back to our memorized order.
Now, as we’ve been doing the previous steps, we should also be thinking about the ‘relationships’ between the cards.
Jacob’s cards are the 2D (19), 5D (25), and 5C (30.)
In this case, I was able to recognize that Jacob’s age (21, although I misremembered it as 20) is close enough that I just need to shift a couple of cards to get his first selection in position to be revealed by dealing cards equivalent to his age. From there, it’s 6 cards to 25 (I spelled ‘Jacob’ for this and misjudged by 1 card), and from there, it’s 5 cards to 30 (I spelled his wife’s name, which conveniently had the exact number of letters I needed.)
That gives you an idea of why it’s hard to describe exactly what to do in the final stage.
If you cannot think of a single way to reveal their cards at the end, just act like it’s a mindreading effect, and name their cards.
That means that the WORST-CASE scenario for this effect is that you impossibly know which cards they picked, even though it was between shuffles and they were free choices. So not bad for a worst-case scenario, huh?
NOTE: Marlo himself had the idea of revealing the 3 cards in interesting ways based on the mem deck, but in his version, the spectators need to call out their cards first.
Fingertip Fumble #2: Sandwich
In this effect, we once again have people pick cards in-between shuffles. This time, not only can you name their cards—but you show that the last two cards have ‘sandwiched’ the first card.
Pit Hartling has a sandwich routine using the memorized deck called ‘Catch me if you Can’ that made me laugh out loud when I saw the audacity of the method. This routine is inspired by that, plus the Marlo ideas discussed above.
Here’s how it works:
You start, once again, in faro 5.
Like in Fingertip Fumble #1 (what a mouthful), you’re going to track the cards as you pass them from one hand to the other.
This first selection really is a free choice. Whatever they pick, you then need to force the two cards that sandwich it in your stack. By the time you faro back into faro 8, the cards will have naturally come together.
Let’s say in the first phase they pick card #41. We now need to force card 42 and 40. We’ll start with 42.
We can do this in one of three ways. If you are well versed in the charts, you’ll know where 42 is in the various shuffles. That’s the goal you should be aiming for.
But if not, you have two options:
- Spread the deck face up toward yourself and catch a break beneath card 42, then do a standard riffle force or dribble force, replacing the card where it came from
- Use a second deck in memorized order and force card 42 from that deck (to justify this, after the first spectator chooses their card, hand them the deck and tell them to ‘guard it.’ of course, you’ll now need a new deck to have the other spectators pick their cards.)
I prefer method 1, since it feels cleaner.
Once we’ve forced 42, we can force 40 in the same way on the second spectator.
Now we can give the deck one more faro shuffle, and all our work will be done. All that’s left is to reveal the names of the cards, and then show that the second two selections have sandwiched the first one.
The nice thing about this is that we can stress how free the first choice is. This way, when people try to think back and wonder if they had a free choice, the ‘freeness’ of the first choice can cancel out the other selections—if one person had a free choice, it stands to reason that everyone did.
Fingertip Fumble #3: ACAAN
This is a perfect example of the ‘technical’ view we talked about in Module 2. We’re going to do the ACAAN routine, but not under any kind of magical context. Instead, we’ll boast that we’re so skilled we can place ANY named card in ANY named position while shuffling the cards.
Which…
Is actually the truth!
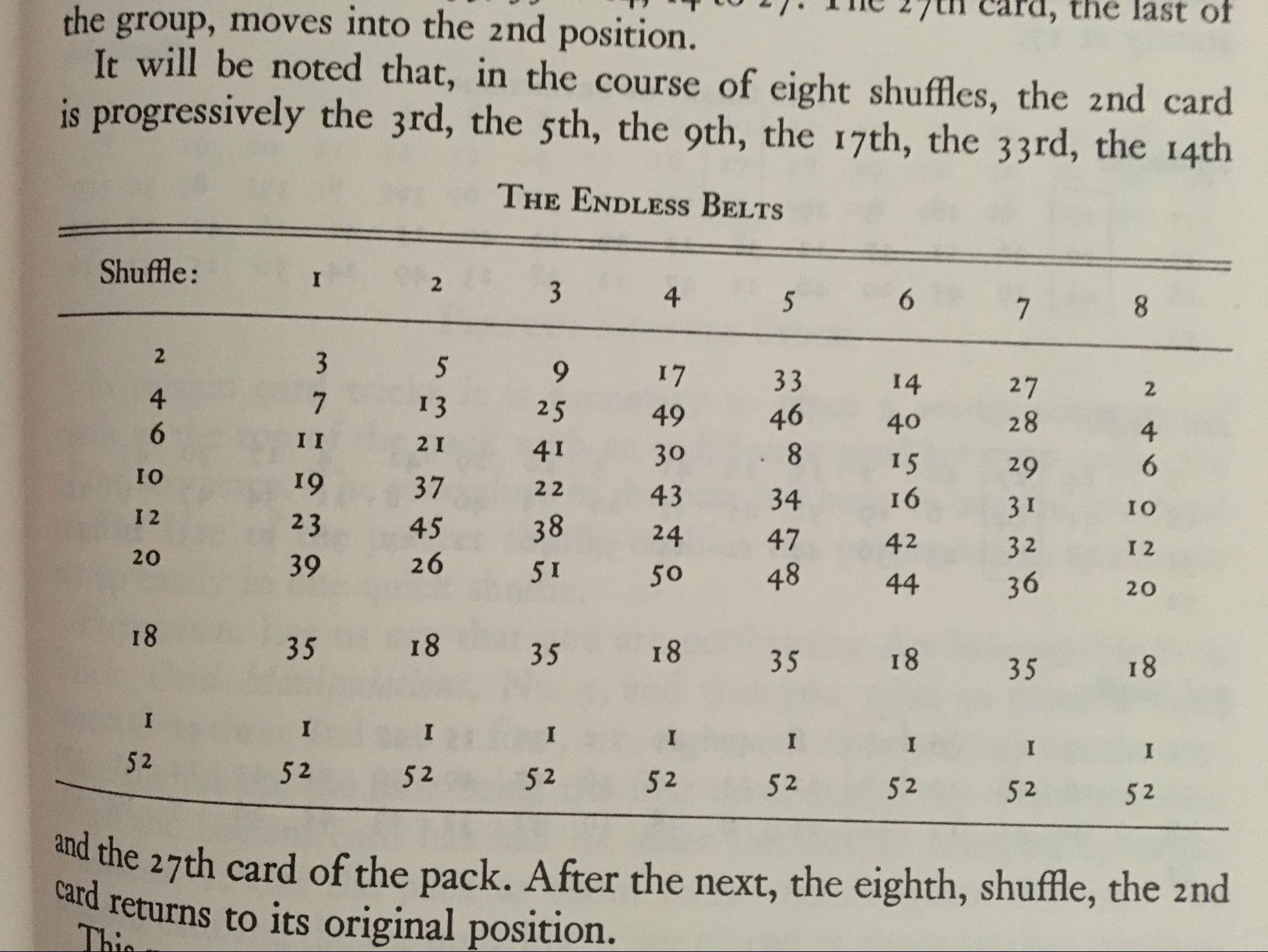
For this one, we’ll be using the ‘endless chains’ chart.
First, we get them to name a card. We then stop thinking about the card by its name and instead think about the number associated with it.
We then find that number on the chart.
We then ask them to name a number. We then find the number they named on the chart. Usually, by shifting one or two cards, we can place their named card at the number in a matter of 1 to 3 faro shuffles.
The nice thing is that we don’t need to ‘secretly’ shift the cards, we can incorporate it into the effect. We can double undercut the appropriate number of cards from top to bottom or vice versa, and it’s completely justified—we’ve TOLD them that we’re going to shuffle their card into position, we’re not acting like it’s already there.
That might seem like I’m making it sound far easier than it is, but in all honesty it’s not that hard.
Let’s look at a couple of examples to see how it would work:
Example 1.
Card: QH (11th card)
Number: 19.
In the Endless Belts chart, we can see that 19 is one faro shuffle away from 10. The QH is currently in position 11. So if we move one card from the top to the bottom via a double undercut, the QH will be the 10th card. At this point, we can give the deck a single faro and their card will be in position 19.
Example 2.
Card: AS (7)
Position 45.
When we find 45 in the chart, we also see 12 two faros to the left. So we could shift 5 cards from the bottom to the top to place the AS in the 12th position, and then do 2 faros to place it in the 5th position.
OR if we look at 7 in the chart, we see that four faros will move it to position 46, at which point we can double undercut one card from the top to the bottom to place it in position 45.
Example 3.
Card: KD (26)
Position: 46
In the chart, we see 25 two faros to the left of 46. We could double undercut one card from the top to bottom (placing the KD in position 25) and then give the deck two faros to place it 46th.
A couple more examples:
Example 4.
Card: 8C (33)
Position: 31
In a case like this, skip the faros and just double undercut two cards from top to bottom.
Example 5.
Card: 8S (22)
Position: 44
In the chart, 23 is one faro to the left of 45. So we can double undercut one card from bottom to top (placing 8S 23rd) and give it one faro (placing it 45th), then double undercut one card from bottom to top (placing it 44th.)
Example 6.
Card: 9D (52)
Position: 50.
Double undercut 2 cards from the bottom to the top. No faros required. Although if you REALLY wanted to, take a look at this:
Find 51 on the chart, and see where it goes after one faro.
That’s right. 50.
So we could double undercut one card from bottom to top (placing the 9D 51st) then give the deck a single faro (placing the 9D 50th.)
Example 7.
Card: 9H (17)
Position: 11
If you look at the chart, we see that after two faros, the card in position 16 moves to 10. So we can double undercut one card from the top to bottom (placing the 9H in position 16), then give two out faros (placing it position 10) then double undercut one card from the bottom to the top (placing it 11th.)
We could go on, but I’ll let you have fun experimenting with this yourself.
The basic idea, as you should now be able to see, is to look at both the number of the card and the position, and try to find the most direct ‘channel’ from one to the other—allowing for a range of numbers we can reach or correct via double undercuts (which again, we are allowed to do, since this whole thing is supposed to be an open display of skill. In fact, you might want to consider doing more false shuffles than you think necessary to give the impression that this is harder than it is!)
A couple of notes:
Since the top card and bottom card are always going to stay in place during out faros, you will need to double undercut at least once or twice to get them ‘in the game.’
If you get someone to name a card BEFORE you tell them what you’re about to present, you should probably just take advantage of the fact they’ve named the top/bottom card and do something magical with that.
The only other exception to this are the cards in position 18 and 35. Those two positions just swap back and forth. Of course, we can move the cards out of those positions via double undercuts, OR we could present this doozy:
This effect uses ideas from page 110 of Mnemonica (‘sha la la la’).
If someone names either the 18th or 35th card (the KC or the KH), you say you’re going to demonstrate your skill at controlling and stacking cards.
First, you need to force the KH or KC, depending on which one has already been picked (force the KH if they picked the KC, force the KC if they picked KH.)
You now want to force the number 17. If you know the toxic force, you could use that using an iPhone calculator, or you could force the 9S and then 8H—adding the two cards’ values together to get 17.
Or if you’re feeling especially bold, ask someone to pick a number ‘between 1 and 20’ and there’s a good chance they’ll say 17
(see Dani DaOrtiz penguin live lecture (3?) for subtleties on this.)
Now tell the audience that you’re going to try to shuffle the two named cards so there’s exactly 17 cards between them.
You can give the deck as many faros as you want, the distance between the two cards will always be 17.
To reveal this, deal the cards face up onto the table and stop when you reach the first selected card. Now count 17 and the next chosen card will show up on the 17th card.
You can now turn the cards face down and place them back on the deck (dealing face up made sure the stack was retained) and do the same thing again, revealing that no matter how many times you shuffle, you can maintain that distance.
NOTE: Each time you faro, the cards swap position. So for our purposes, we could give them one faro or three faros and we’d get the same result (the cards swap, or the cards swap/swap back/swap.)
You can weave in false shuffles in between the faros to misdirect from the fact we’re reliant on the faros to accomplish this.
Make sure you start dealing at the new 18 (not from 35 to 18, from 18 to 35. – this means you’ll start at alternating cards each time.)
NOTE: If you ask someone to name a number ‘between 1 and 20’ but they don’t say 17, you’re still covered for a few of the other possibilities:
- If someone says 16, you can deal 16 and then turn over the next card (card #17) and it feels natural
- If they say 18 then start by counting the first selected card as card #1, the next selected card will show up on #18
- If they say 15, count 15 and then do a double lift
- If they say 14, count 14 and do a triple lift
In all honesty, I’d just do the first method and double undercut some cards to get the cards into position for controlling via faros.
NOTE: If you so desired, you could do the ‘spectator faro’ (either with two spectators or one spectator and you) and change the presentation slightly. Instead of controlling a card to a position, tell them you can track cards even when other people are shuffling. Once they name the card, find it on the chart and look at the position after one faro. This is where the card will be after they finish the faro.
NOTE: How do we get away with using the chart?
Two ideas. First, learn it.
Yes…I know. More memorizing. But having this kind of chart handy in your mind is incredibly useful.
But don’t worry. In the meantime…
Pit Hartling, a constant source of excellent ideas, has a routine called the ‘Poker Formulas.’
In this routine, someone names any poker hand, and after consulting a ridiculously huge sheet of ‘formulas’, Pit is able to deal the hand called for.
It’s very funny, but little do they know that the ‘poker formulas’ he’s looking at really ARE poker formulas. Of course, I won’t get too deep into Pit’s methods, but the basic premise could play well here too.
Some ‘cheating formulas’ sheets with our endless chain chart and shuffle charts printed all over them could be a handy prop that looks so ridiculous people don’t take it seriously…when in fact it’s exactly what we need.
We’d likely need to switch out some of the words like ‘5th shuffle’ for ‘5’, and so on, but I think there’s a possibility there.
One final note might be to have the charts encoded on the back of an ad card that we can have lying around. If we’re using this card specifically for the first two fumbles, we only need the charts for the 5th, 6th and 7th shuffle (the 8th is your memorized order so you don’t need a chart for that.) I’m sure some creative magicians could find a way to get that info encoded on the bottom of a card box too. If you want to save even more space you could only list the first 26 numbers of each chart, since the vast majority of the time they’re going to stop you within the first 26. (heck, use the first 13 if you think you can get away with that.) If they don’t, find an excuse to start dealing again. (I will leave that challenge to you, dear reader.)
NOTE: Marlo gives a formula on page 15 of Faro Notes that explains how to track the position of a card after a set number of faro shuffles. Check it out if you’re interested since it’s a fascinating idea, but it does require some mental maths.
Now that we’ve had some fun with fumbles, let’s look at a mystifying display of card cheating…
